„Die größte Erfindung des menschlichen Geistes? – Die Zinseszinsen!“ – Albert Einstein
In meinem ersten Basiswissen-Artikel ist es mein Ziel euch auf eine anschauliche Art den Zinseszinseffekt (oder auch einfach nur: Zinseszins) näherzubringen und euch aufzuzeigen, warum er für einen nachhaltigen und langfristigen Vermögensaufbau so immens wichtig ist.
Was ist der Zinseszinseffekt?
Um den Zinseszinseffekt zu erklären muss man als erstes den „einfachen“ Zins verstanden haben. Der einfache Zins ist nichts anderes als die Entschädigung, die jemand dafür verlangt (bzw. erhält), wenn er sein Geld einem Zweiten zur Verfügung stellt. Das klassische Beispiel ist dafür das Festgeldkonto. Wir legen unser Geld für eine gewisse Zeit von ein paar Jahren (fest) an und erhalten dafür, als Entschädigung da wir in diesem Zeitraum nicht an unser Geld herankommen, einen vorher festgelegten Zins. Die genaue Ausgestaltung der 
Zinsen hängt immer von der getätigten Anlage ab. Normalerweise werden die Zinsen jedoch als ein Prozentsatz von der gesamten Anlagesumme festgelegt und quartalsweise oder jährlich ausgezahlt. Ein kleines Beispiel: Wir legen 10.000€ zu einem Zinssatz von 10% bei unserer Bank für 20 Jahre als Festgeld an: Dann erhalten wir beispielsweise jedes Jahr zum Jahreswechsel 1.000€ an Zinsen auf unser Girokonto überwiesen. Wichtig ist hier, dass die Anlagebasis also die 10.000€ immer gleich bleiben, da die Zinsen ja ausgeschüttet werden.
Der Zinseszinseffekt funktioniert allerdings auch bei allen anderen Formen der Geldanlage. Die langfristige Rendite des Aktienmarktes beträgt beispielsweise ca. 7%. Die Entwicklung verläuft jedoch mit der Zeit nich immer gleichmäßig.
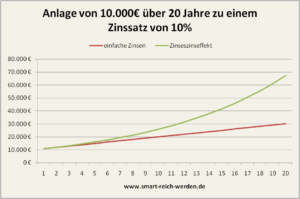
Das waren soweit die einfachen Zinsen. Beim Zinseszinseffekt verhält es sich etwas anders, die angefallenen Zinsen aus dem ersten Jahr werden in diesem Fall nicht an uns ausgeschüttet sondern zu den bereits angelegten 10.000€ hinzuaddiert. Nach einem Jahr haben wir also einen Betrag von 11.000€ auf unserem Festgeldkonto. Wenn das zweite Jahr abgelaufen ist werden somit nicht mehr die 10.000€ sondern die 11.000€ verzinst. Unsere Anlagebasis hat sich erhöht und wir erhalten 1.100€ an Zinsen. Beim Zinseszinseffekt erhöht sich die Anlagebasis also jedes Jahr um die angefallenen Zinsen. Die große Stärke des ganzen ist aber die Mathematik. Durch die Wiederanlage der Zinsen steigt das Vermögen nicht mehr linear (als Gerade) sondern exponentiell (eine nach oben hin steiler werdende Kurve). Ich denke der Unterschied wird in der Grafik unten sehr schnell deutlich. In der Tabelle erkennt man schön, dass wir durch den Zinseszinseffekt einen Vorteil von 37.275€ gegenüber dem einfachen Zins haben.
Wie lässt sich der Zinseszins berechnen?
Im nächsten Schritt wollen wir natürlich vor der Geldanlage wissen was für Auswirkungen wir durch den Zinseszinseffekt erwarten können ohne jedesmal eine große Excel-Tabelle erstellen zu müssen. Dafür ist leider ein kleiner Einstieg in die Mathematik erforderlich, aber so schwer ist es auch nicht. Eigentlich ist nur eine einfache Formel zur Berechnung des Zinseszinseffekts notwendig:
- Smartbroker (Ab 0 Euro pro Order handeln)
- Trade Republic (Aktien & ETFs provisionsfrei handeln)
- Consorsbank (20 Euro für deinen ersten Sparplan geschenkt)
- comdirect-Depot (Mein kostenloses Allrounder-Depot)
- DKB-Cash (dauerhaft kostenloses, verzinstes Girokonto)
- Weltsparen (Automatisches Parken der Cash-Reserve)
Diese Formel angewendet auf unser Beispiel von oben sieht dann so aus: 
Unser Endkapital in Höhe von 67.275€ lässt sich auch oben in der Tabelle wiederfinden.
Wie ihr seht lassen sich leichte Zusammenhänge schnell im Taschenrechner lösen, für kompliziertere Umstellungen oder die Berücksichtigung von Steuern nutze ich meist einen Online-Zinseszins-Rechner.
Wie hängen Zinseszinseffekt und Vermögensaufbau zusammen?
Oben habe ich euch gezeigt, was der Zinseszinseffekt überhaupt ist und wie er berechnet wird. Ich glaube dabei ist klar geworden, was Albert Einstein meinte, als er den Zinseszinseffekt als das achte Weltwunder bezeichnet hat.
Der Vermögensaufbau beginnt also sehr langsam, bzw. gleichmäßig. Nach einiger Zeit jedoch spielt der Zinseszinseffekt seine Stärke aus und beschleunigt das Vermögenswachstum. Daraus folgt, dass auf der einen Seite immer Geduld eine große Rolle für den Vermögensaufbau spielt. Auf der anderen Seite kann Geduld aber nur derjenige haben, der möglichst früh mit dem Vermögensaufbau beginnt. Es gilt also die drei Faktoren, die den Erfolg des Vermögensaufbaus bestimmen schon in frühen Jahren so gut es geht zu optimieren.
Zum Abschluss noch ein paar kleine Beispiele, was der Zinseszinseffekt aus 10.000€ und 50.000€ machen kann, wenn man früh genug mit dem Vermögensaufbau beginnt.
[ratings]
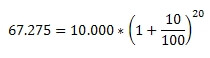
Julia Heinemann meint
Hey Jan,
eine super Seite! Auch für mich als Einsteiger so aufgebaut, dass ich mich gerne mit dem Thema befasse. Danke dir!
LG, Julia
Jan meint
Vielen Dank, ich freue mich natürlich immer über Lob und Kritik
VG
Jan
Dividenden-Sammler meint
Hallo Jan,
ich glaube, das Du ein schlauer Kerl bist!
Deswegen habe ich eine Frage und hoffe, das Du sie beantworten kannst:
Ich habe zwar eine Antwort im Kopf, würde sie aber gerne unabhängig von Dir verifizieren lassen.
Das mit dem Zinsesszinseffekt ist klar und eindeutig! Absolut das Beste was es gibt!
Nun die Frage: Hast Du eine Formel parat, die Zinseeszins + eine jährlich steigende Einzahlung vereint?
Io ist also nicht konstant, sondern steigt jedes Jahr (der Einfachheit halber immer um den selben Betrag).
Wie würdest Du so etwas berechnen?
Herzliche Grüße
Dividenden-Sammler
Jan meint
Hall Dividenden-Sammler,
ich muss zugeben, dass ich die Formel dafür nicht sofort im Kopf habe. Wie würde ich es berechnen? Mit diesem Link: http://www.zinsen-berechnen.de/sparrechner.php
Irgendwo sind da auch noch Erklärungen zur Berechnungsweise, die konnte ich aber leider gerade nicht finden.
Ich hoffe du bist mit meiner Antwort trotzdem zufrieden 😉
VG Jan
Dividenden-Sammler meint
Hallo Jan,
vielen Dank für Deine Antwort.
Die Dynamik erhöht die Rate Sparrate – aber in dem Fall nur prozentual. Damit würde der Betrag jedes Jahr größer werden, weil die Dynamik immer auf das letzte Jahr gerechnet wird.
Aber vielen Dank – es geht auf jeden Fall mal sehr stark in diese Richtung.
Ich habe eine Formel gefunden, ist aber schwer zu verstehen:
k = die Steigerungsrate pro Jahr, a = Startguthaben, x = die Startrendite
Betrag = a * 1 .0x ^ ( Jahre + k * Jahre^2 /2)
Ich werde mal sehen, was ich noch alles finden kann…
Beste Grüße
D-S
Jan meint
Stimmt, das ist eigentich blöd gemacht. Sonst simuliere ich soetwas auch immer ganz gerne mit Excel und berechne dann den internen Zinsfuß. Man sollte sich da aber auch der Vor- und Nachteile des IZF bewusst sein.
Dummerchen meint
Jetzt muss ich mal ganz neugierig nachfragen: Was ist denn der Nachteil des IZF? Ich bevorzuge den IZF eigentlich für alle erdenklichen Berechnungen.
Gruß
Dummerchen
Chris von gieristgut.com meint
Das Problem beim internen Zinsfuß ist, dass es auch zu 2 oder mehreren Ergebnissen kommen kann. Beispielsweise bei einem Polynom 2ten Grades.
Außerdem sagt der IZF auch nichts über die Kapitalbindung aus. Das kann bei einer Investition (nicht bei Wertpapieren) zu einem Problem werden.
Ein weiterer Punkt ist, dass eine einheitliche (gerade) Zinsstrukturkurve angenommen wird.
Viele Grüße
Dummerchen meint
Und, passt die Formel auch zu Deinem Problem? Woher hast Du sie denn?
Wofür braucht man denn die 1.0 in der Formal und heißt der hintere Teil der Formel k/2*jahre^2 oder worauf bezieht sich das „/2“?
Gruß
Dummerchen
Dividenden-Sammler meint
Die 1.0 hängen mit dem Startzins zusammen. Korrekterweise heißt es 1.0x (wobei x nicht multiplizieren bedeutet). Sondern wenn der erste Zins bei 5 Prozent liegen würde, muss man anstelle des X eine 5 einsetzen. Es würde dann so aussehen: 1.05.
Den letzten Teil der Formel kann ich nicht erklären. Ich habe gesucht, gefunden und es passt.
Aber WARUM es so ist – das muss ein Mathematiker erklären – mir ist das zu hoch (hoch^2 😉 )
Grüße
D-S
Christoph meint
Hallo Jan,
ich muss dir jetzt mal ein Kompliment machen!
Was du schreibst, gibt es sicher auch auf zig anderen Blogs zu finden, was mich jedoch echt anspricht und was ich so selten finde, ist: Du bringst die Sachen super verständlich für einen Neuling in Sachen ETF/Aktien/Zinseszins etc. rüber!
Bei deinen Artikel bin ich nicht ausgestiegen, sondern das hat mich jetzt sehr motiviert, auch anzufangen mit einem ETF-Sparplan. Nischenseiten sind schön (eine meiner Seiten siehst du im Link ;)), doch wie in einem deiner anderen Artikel diskutiert, sind sie auch viel Arbeit, und eine Streuung der Einnahmen ist sicher nicht verkehrt.
Ich freue mich auf weitere Artikel von dir.
Lg, Christoph
Dario meint
Hallo Jan,
ich bin Anfang 20 und an Geldanlagen interessiert.
Zurzeit investiere ich in 2 Aktienfonds (ein VL.-Vertrag) und in einen, den ich mit 1000€ verteilt auf 10 Monate (also 100€ im Monat bespare) . Bei letzterem handelt es sich um den DWS Top Dividende. Es handelt sich um einen ausschüttenden Fonds.
Nun meine beiden Fragen. 😀
Ich habe mir überlegt die Dividende nicht auszahlen zu lassen, sondern diese gleich wieder dafür zu verwenden neue Anteile des Fonds zu kaufen. Quasi aus dem ausschüttenden Fonds ein thausierenden Fonds zu machen. Was hälst du davon ? Würde ich damit den Zinseszinseffekt nicht mir zu Nutze machen ?
Die 2.Frage lautet: Wie würdest du 7000€ anlegen ?
Würde mich sehr über eine Antwort freuen
LG
Jan meint
Hallo Dario,
was genau meinst du mit nicht auszahlen lassen?
Die Wiederanlage ist die Grundvoraussetzung für den Zinseszinseffekt.
Die sofortige Wiederanlage macht aber in Hinblick auf den Zinseszinseffekt auf jeden Fall Sinn.
Die zweite Frage ist schwierig. Ich kenne deine Gesamtsituation nicht. Schau dir mal diesen Beitrag an:
https://mission-rendite.de/etf/etf-sparplan/
Gerne kannst du auch in unserer Community bei Facebook Fragen stellen: https://www.facebook.com/groups/smart.reich.werden/
VG
Dario meint
Hallo Jan,
danke für die schnelle Antwort. 😊
Mit nicht auszahlen meinte ich, dass ich die Dividende, die Ausgeschüttet wird, mir nicht auf eins meiner Konten auszahlen lasse, sondern die Bank beauftrage, die Dividende sofort wieder in den selben Fonds zu reinvestieren. Ich würde mit der ausgezahlten Dividende sofort wieder Anteile des Fonds kaufen.
Danke für die Verlinkung zu der 2. Frage !
Liebe Grüße
Dario
Jan meint
Ok, verstanden.
Ja, macht auf jeden Fall Sinn.
Pass nur auf, manche Banken nehmen bei sowas Gebühren.
Unter Umständen auf dem Konto sammeln und manuell anlegen.
VG
Rainer Neugebauer meint
Warum sind eigentlich die Kurven in der Grafik, die den Zinseszins-Effekt verdeutlicht, nur 19 Jahre lang?
Jan-Christian meint
Eine sehr gute Frage. Mir ging es damals um die Darstellung des Unterschieds zwischen exponentiellem und linearem Wachstum. Der Beitrag steht aber auf der „zu aktualisieren“ Liste. ich nehme das mal mit als Änderungspunkt auf.
Stefan meint
Hey Christian,
ich bin auch der Meinung, dass der Zinseszinseffekt der Turbo für den Vermögensaufbau ist. Aufgrund des exponentiellen Wachstums wird gerne unterschätzt, welche Kraft der Effekt hat.
Insbesondere die Anlagedauer hat einen großen und nicht zu unterschätzenden Einfluss auf den Zinseszinseffekt. Daher gilt: Je früher man anfängt zu investieren, desto besser.
Gruß Stefan
Jan-Christian meint
Hallo Stefan,
absolut. Früh anfangen ist wichtig. Ich finde aber die Höhe des Anlagebetrags und die Rendite noch viel wichtiger, das sie im Gegensatz zur Zeit durch uns beeinflussbar sind.
VG